
OPENING QUESTION: What is the unit vector ![]() , and why do we care?
, and why do we care?
LEARNING OBJECTIVES:
I will be able to find the center of mass of several particles using algebra during today's class.
I will be able to find the center of mass of an 'extended' object using calculus during today's class.
FORMULAE OBJECTUS:
-
p = mv
-
J = F∆t = ∆mv = ∆p
-
∫Fdt = ∆p
-
∑F = dp/dt
-
m1v1i + m2v2i = m1v1f + m2v2f'
-
xcm = (m1x1 + m2x2)/(m1+m2) (2 body system)
-
xcm = ∑mixi/(M) where M is the mass of all parts of a multi-body system
-
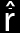 cm =1/M∫
cm =1/M∫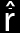 dm the center of mass of a solid object
dm the center of mass of a solid object
∆ptotal = J Impulse-momentum theory
WORDS O' THE DAY:
-
momentum (p)
impulse (J): "A measure of the degree to which an external force changes the particle's momentum". Note: Our book uses the term (I) to denote impulse, but that's not standard since (I) usually stands for the moment of Inertia (as we'll see in the next chapter). The AP Equation Sheet uses J to denote impulse.
conservation of linear momentum
-
Newton's 2nd Revised: ∑F = dP/dt (the sum of the forces acting on a particle (or system) is equal to the change in momentum with respect to the time in which those forces acted)
-
elastic collisions: Objects collide and then separate -- kinetic energy and momentum are BOTH conserved
-
perfectly inelastic collisions: Objects collide and then stick together -- momentum IS conserved but kinetic energy is not
-
inelastic collisions: Objects collide but do not stick together -- momentum IS conserved but kinetic energy is not
═══════════════════════════
WORK O' THE DAY:
Let's get our first presenter up here
Now the second
CALENDAR: TEST ON FRIDAY
Let's push the envelope just a wee bit. I'm thinking 10 problems in....?
═══════════════════════════
We will occasionally have to deal with systems of MANY particles where some sort of force is acting on all particles at once (think fireworks!).
It turns out that we can use IMPULSE to evaluate the result of a force acting to change the momentum of each of the particles thusly:
∆ptotal = J
Let's see if we can use that to evaluate Sophia's thought experiment from yesterday:
You're driving down a two lane road late at night. You pass over a small rise and see a car in your lane coming straight at you. Do you:
1) collide straight into that car
2) swerve off and collide straight into a stone wall.
assume ∆t is the same in both instances.
Use SPECIFIC real world-ish data to support your claim.
═══════════════════════════
pour moi:
- mass of each of two 2016 Scion FRS's: 1250 kg
- velocity of each car (45.0 mph each): 20.1 m/s
Scenario #1: 1 car vs 1 (non-moving) stone wall:
∆ptotal = J
car goes from 45.0 mph to zero:
∆pcar = (1250 kg)(20.1 m/s) → 0 mps
change in momentum = impulse = F∆t
∆pcar = F∆t
Assume brief ∆t (.030 sec)-- Solve for the force of the impact on the driver:
(∆pcar)/(∆t) = F
(1250 kg)(20.1 m/s)/(.03sec)
= 837,500 N
TWO CAR SCENARIO:
∆pcars = I
(∆pcars)/(∆t) = F
Each car has the same change of momentum in the same amount of time so:
(2∆pcar)/(∆t) = F
(2)(1250 kg)(20.1 m/s)/(.03sec) = F
F = 1,675,000 N
BOO!
Let's try a demo: Use the impulse-momentum theorem to explain the following:
═══════════════════════════
Work through the exploding projectile problem 9.13 & 9.14 on page 274. They do a MUCH better job of using the main info in that unit than the problems in the book.